A Gentle Introduction to Comonads
Justin Heyes-Jones
Software Developer

Properties of pure functions
A => B
Total
Deterministic
No side effects
Advantages of Pure Functions
Easy to test
Equational reasoning
Composable
Pure Functions need help
Side effects (IO)
Partiality (Option)
Exceptions (MonadError)
Nondeterminism (List)
Mutable state (State)
Type classes
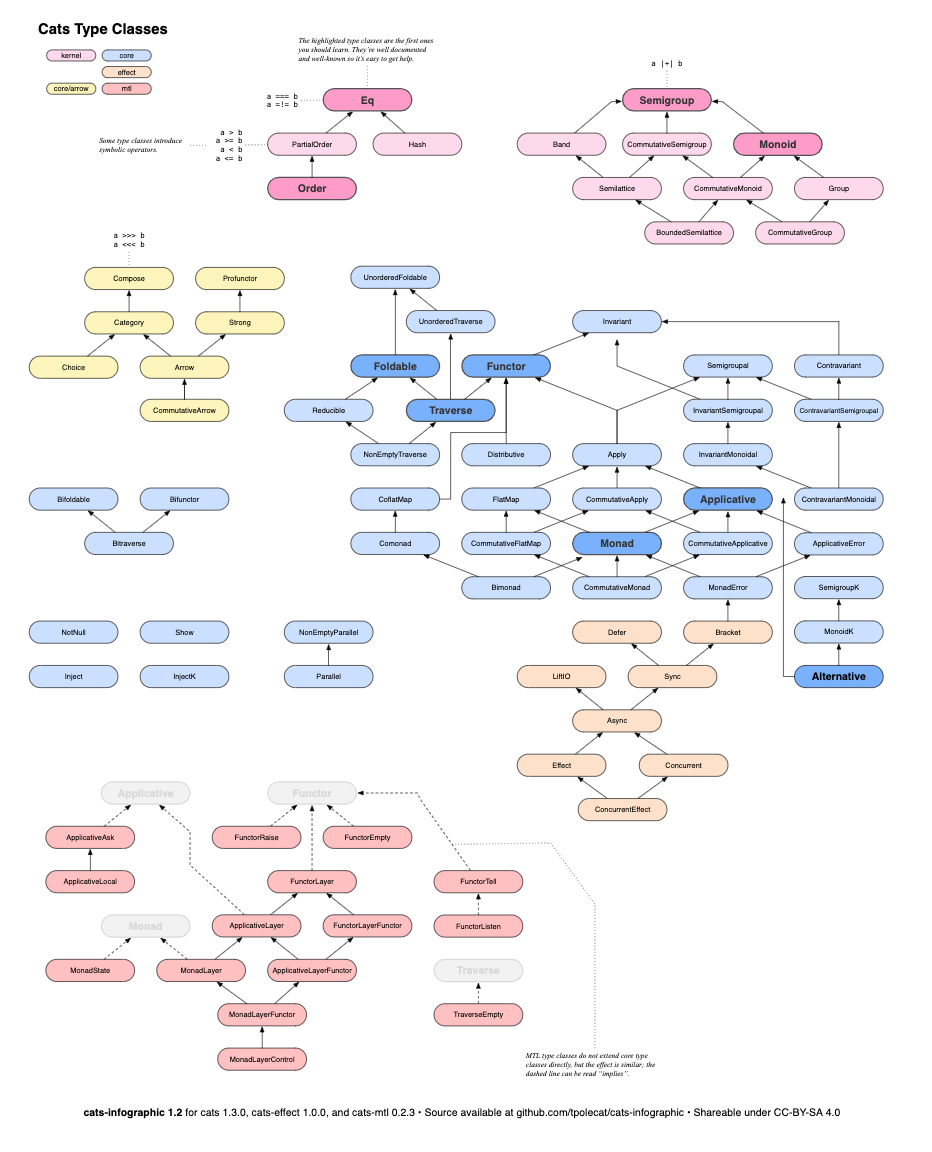
Functors, Monads and Comonads
Functional Programming with Effects - Rob Norris
"Find Functor, find Monad and see what's nearby"

Scala
Type classes are typically implemented as traits
trait Show[A] {
def show(a: A): String
}
Show example
import cats._
import cats.syntax.show._
case class Person(name: String, yearOfBirth: Int)
implicit def showPerson = new Show[Person] {
def show(p : Person) = s"Person: ${p.name} born ${p.yearOfBirth}"
}
Person("Bob", 1989).show
// res5: String = "Person: Bob born 1989"
Functor
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A -> B): F[B]
}
Functor - example
Maps value of type A in a list to values of type B in a new list
import cats._
import cats.implicits._
List("Hello", ",", "how", " ", "are", "you", "?").map(_.size)
// List[Int] = List(5, 1, 3, 1, 3, 3, 1)
Monad
trait Monad[F[_]] extends Functor[F] {
def pure[A](x: A): F[A] // Also known as unit and return
def flatMap[A, B](fa: F[A])(f: (A) ⇒ F[B]): F[B] // (also bind)
}
Monad - Pure
pure simply constructs the effect with a pure value of type A
10.pure[List]
// List[Int] = List(10)
Monad - FlatMap
Flatmap lets us compose functions that take pure values and produce new values in some effect context
def intToDigits(n: Int) : List[Int] =
n.toString.toList.map(_.toString.toInt)
intToDigits(1001)
// List[Int] = List(1, 0, 0, 1)
def intToRepeatedInt(n: Int) : List[Int] =
List.fill(n)(n)
intToRepeatedInt(5)
// List[Int] = List(5, 5, 5, 5, 5)
intToDigits(12345).flatMap(intToRepeat)
// List[Int] = List(1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5)
Monad - FlatMap
With only map we get a nested result, usually not what we want...
intToDigits(12345).map(intToRepeat)
// List[List[Int]] = List(List(1),
// List(2, 2),
// List(3, 3, 3),
// List(4, 4, 4, 4),
// List(5, 5, 5, 5, 5))
Flatmap is a MAP followed by a FLATTEN
List[List[Int]] => List[Int]
F[F[A]] => F[A]
Comonad
trait Comonad[F[_]] extends Functor[F] {
def extract[A](x: F[A]): A
def coflatMap[A, B](fa: F[A])(f: F[A] => B): F[B]
}
Comonad - extract
Monad: pure
A => F[A]
Comonad: dual of pure is extract
F[A] => A
Comonad - Extract
import cats.data.NonEmptyList
val nel1 = NonEmptyList.of(1,2,3,4,5)
// NonEmptyList[Int] = NonEmptyList(1, List(2, 3, 4, 5))
nel1.extract
// Int = 1
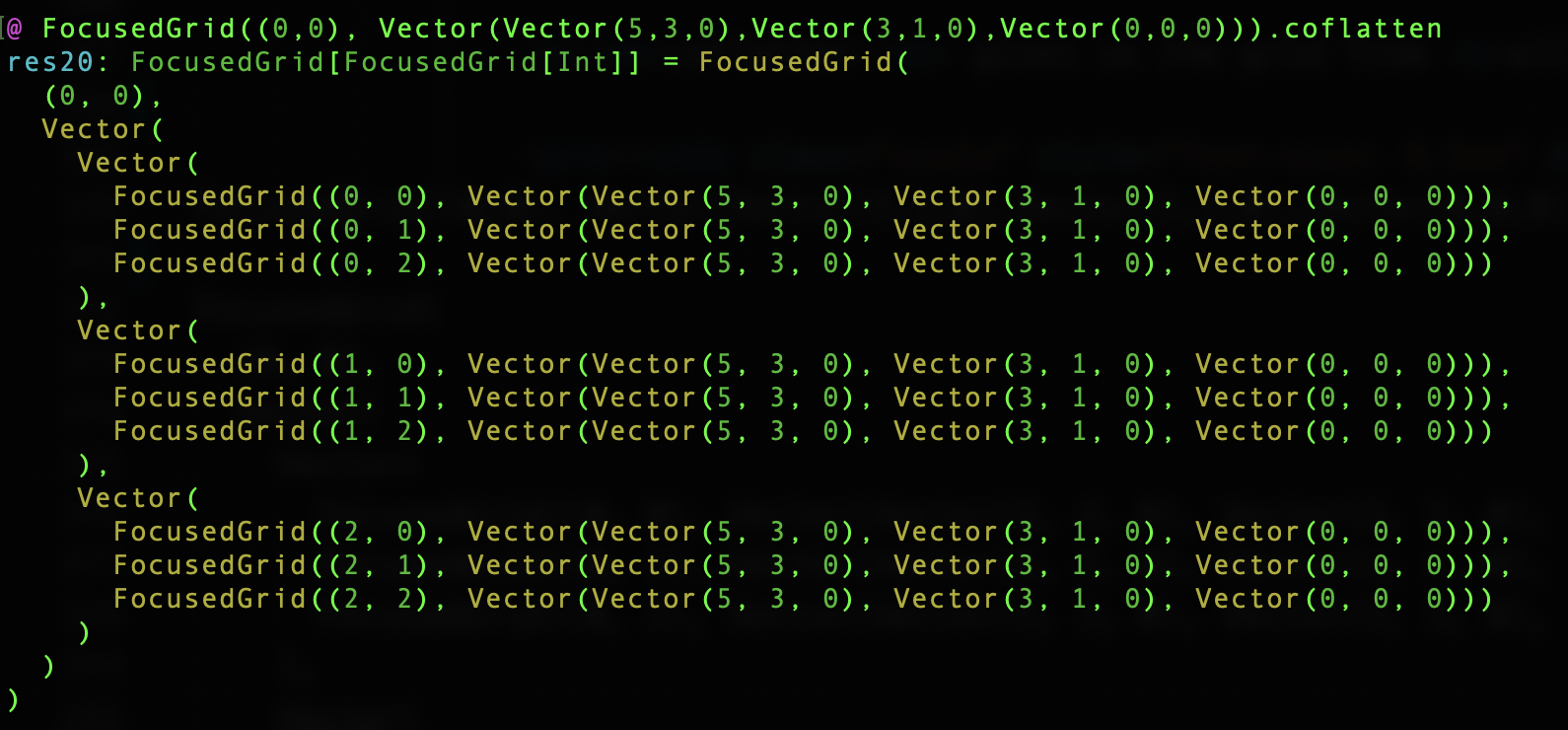
Comonad - Unflatten
Unflatten is not part of Comonad's interface, but useful to understand coflatMap
def coflatten[A](fa: F[A]): F[F[A]]
val nel1 = NonEmptyList.of(100,200,300,400,500)
// NonEmptyList(100,200,300,400,500)
nel1.coflatten
// NonEmptyList(
// NonEmptyList(100,200,300,400,500)
// NonEmptyList(200,300,400,500)
// NonEmptyList(300,400,500)
// NonEmptyList(400,500)
// NonEmptyList(500))
Comonad - coflatMap
NonEmptyList.of(100,200,300,400,500).
coflatMap(list => list.toList.sum)
// NonEmptyList(1500, 1400, 1200, 900, 500)
Comonad - coflatMap
One of the comonad laws specifies...
NonEmptyList.of(100,200,300,400,500).coflatMap(_.extract) ==
NonEmptyList.of(100,200,300,400,500)
Which is why extract and coflatmap were implemented that way
Focused Grid
Represent a 2d array and a focus point
case class FocusedGrid[A](
focus: Tuple2[Int,Int],
grid : Vector[Vector[A]])
Focused Grid
extract gives the grid value at the focus
coflatten gives us the grid from all focus points
Focused Grid
Box filter
Take an average of a box of pixels around the focus point
def boxFilter(width: Int):
FocusedGrid[(Int, Int, Int)] => (Int, Int, Int) =
{ fg =>
val widthSqr = width * width
val sum = localSum(fg, (255, 255, 255), width)
((sum._1 / widthSqr).toInt,
(sum._2 / widthSqr).toInt,
(sum._3 / widthSqr).toInt)
}
No filtering

Box filter width 5 pixels
originalImage.coflatMap(boxFilter(5))

Box filter width 15 pixels
originalImage.coflatMap(boxFilter(15))

Compose a sequence of transformations
originalImage.
coflatMap(boxFilter(9)).
coflatMap(mirrorHorizontal)

Transform into two images then merge them
val ck1 = Cokleisli(mirrorVertical)
val ck2 = Cokleisli(mirrorHorizontal)
val ck1ck2Compose = ck1.
product(ck2).
map(blendTuple)
val ck1ck2ComposedProcess = originalImage.
coflatMap(ck1ck2Compose.run)
Transform into two images then merge

Conway's Game of Life
def conwayStep(fg: FocusedGrid[Int]): Int = {
val liveNeighbours = localSum(fg)
val live = fg.extract == 1
if(live) {
if (liveNeighbours >= 2 && liveNeighbours <= 3)
1
else
0
} else {
if (liveNeighbours == 3) 1 else 0
}
}
// start.coflatMap(conwayStep).map(a => prettify(a)).show
Conway's Game of Life