Functional Error Handling with Applicative in Scala 3

This is a companion blog my sixth Functional Justin YouTube video which you can find here: https://youtu.be/3GPXEzO14ZE

In the video I talked about the Functor Laws and continued working on the example program that evaluates arithmetic expressions. I use Monad, then Applicative, to show how we can make a Numeric instance for Either, so we can handle errors in a nice functional way.

Since the episode I spent a bit of time cleaning up the code and putting what we already saw (Numeric and Functor) into their own packages. I also went ahead and implemented Applicative and Monad which will be used in the the video and below.

You can find the typeclasses here:

https://github.com/justinhj/evalexample/tree/video6/src/main/scala/org/justinhj/typeclasses

Our Functor type class really only exists to implement the map function, and we already have a map function in the Scala standard library for such things as Options, Lists and Futures. You might wonder why we would go the trouble of making our own abstraction just to write a function that we already had.

The goal of abstractions like Functor is not just to provide useful functions like map, but to provide a principled layer that we can build further abstractions upon. For example we will see that Applicative can be built on top of Functor, Monad on top of Applicative, and this is only possible because Functor behaves in accordance to strict rules that it brought with it from Category Theory.

You can read more about Functors on the Haskell documentation pages:

https://wiki.haskell.org/Functor

Another great resource is the famous "red book"…

https://www.manning.com/books/functional-programming-in-scala

The following code implements an arithmetic expression evaluator using the Numeric type class developed in a previous video and adds error handling by using Either. Each step of our evaluator has this signature.

type WithEnv[A] = Env[A] ?=> Either[EvalError, A]

Which means it is a function takes an input environment (our symbol table) as an implicit argument, and returns an Either where the error (or Left) type is EvalError. EvalError represents the different errors our code will handle. It is a sum type implemented as a Scala 3 enum (seen in a previous video).

enum EvalError {
  case InvalidSymboName
  case SymbolNotFound
}

In previous blogs/videos I showed how we can implement a Numeric instance so we can do arithmetic on many different types, just so long as we create an instance of Numeric to handle them. Now we must implement Numeric for the following type Numeric[Either[EvalError, A]].

The instance signature is

given evalResultNumeric[A: Numeric]: Numeric[Either[EvalError, A]] with {

Now we must implement the methods of Numeric. Because our numeric values are inside the EvalResult (an Either) we can't just implement the multiply directly. We need a way to get inside it. As we saw in the previous blog/video, Functor gives us a way to apply a pure function to an effect. Since mul is a pure function, maybe we can use it?

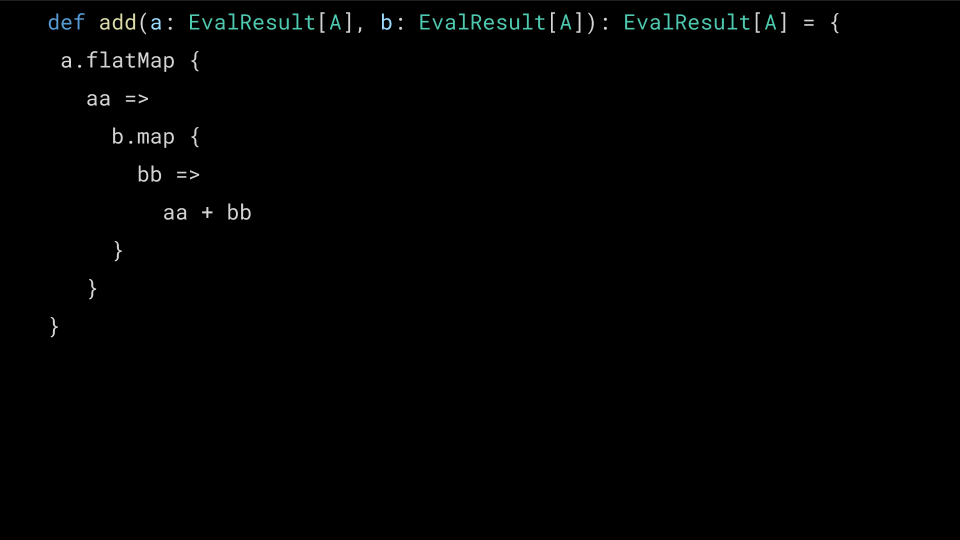
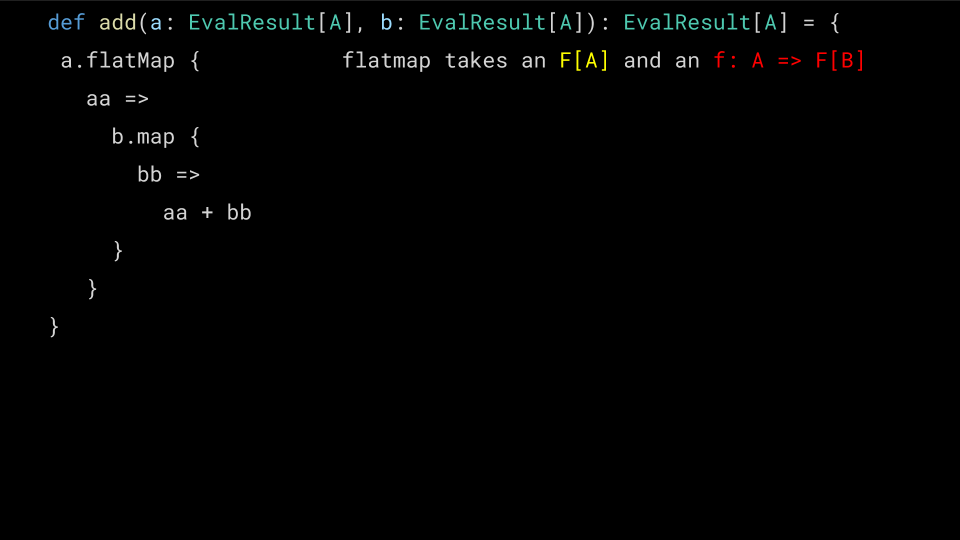
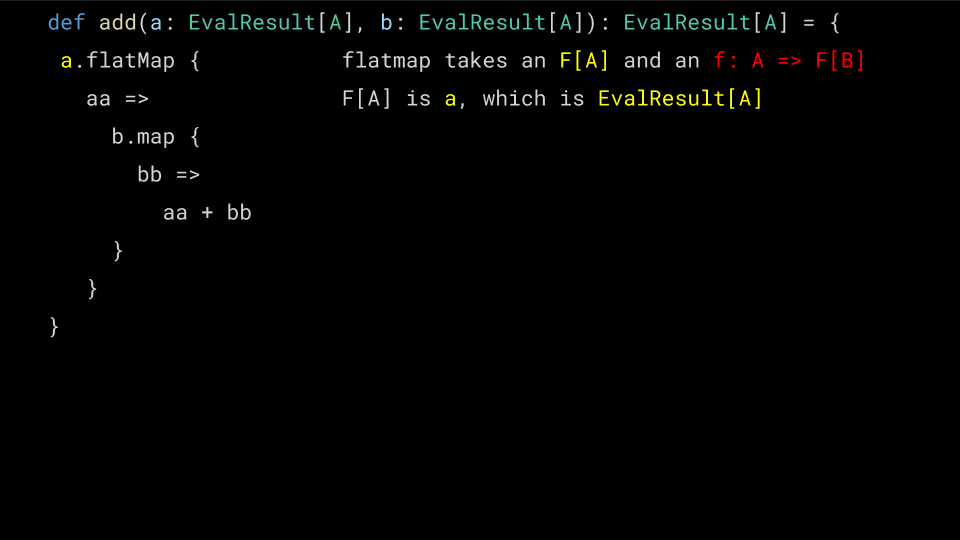
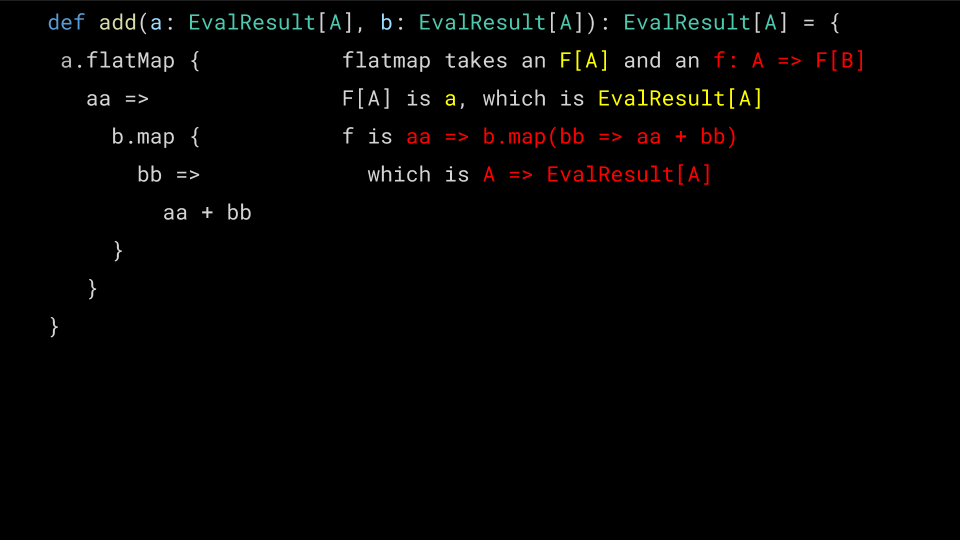
def mul(a: EvalResult[A], b: EvalResult[A]): EvalResult[A] = {
  a.fmap { // DOES NOT COMPILE, WRONG TYPE
    aa => 
    b.fmap {
      bb =>
        aa * bb
    }
  }
}

Note I am using the name fmap and fflatMap to make it clear we are not using the standard library implementations here. This is just for clarity but is not a good practise because, for example, you will lose the ability to use for comprehensions.

What went wrong here is that Functor's map operation has the signature

extension [A, B](x: F[A])
  def ffmap(f: A => B): F[B]

which means it takes our Either[EvalError, Numeric[A]] and a pure function, which it will apply to the Numeric. Unfortunately we end up with an extra layer of Either! Let's see why…

So instead of Functor with its map function, we need Monad and its flatMap which let's us implement all the arithmetic functions in a straightforward manner.

https://github.com/justinhj/evalexample/blob/video6/src/main/scala/org/justinhj/typeclasses/monad/Monad.scala

I've implemented Monad in the file above and made it available to the code. The implementation is simple and based on the example given in the Dotty documentation. The main difference is I've also implemented Applicative, since we will use that in a moment, and Monad extends Applicative.

https://dotty.epfl.ch/docs/reference/contextual/type-classes.html

Now each arithmetic operator can be implemented as follows, which achieves our goal of being principled and functional and let's us handle errors at the type level.

def mul(a: EvalResult[A], b: EvalResult[A]): EvalResult[A] = {
  a.fflatMap {
    aa => 
      b.map {
        bb =>
          aa * bb
      }
  }
}

What we have at this point is a nice implementation of Numeric that uses Either's for error handling, which in turn is built on Applicative. Let's see how easy it is to add new errors and capabilities to the expression evaluator.

enum EvalError {
  case InvalidSymboName
  case SymbolNotFound
  case DivisionByZero
}

First we add a new error type DivisionByZero. The next thing we need is for Numeric to have a concept of whether a number is zero or not. Remember that we can implement Numeric for many different types and not all of them represent zero the same way. We can therefore add an isZero predicate to the type class.

def isZero(a: T): Boolean 

Next every instance of Numeric needs an implementation of it, so for exapmle in the Int instance we have the following.

def isZero(a: Int) = a == 0

The implementation for Numeric Either let's us write the isZero for any value in an either as long as that value has a numeric instance of its own.

given evalResultNumeric[A: Numeric]: Numeric[Either[EvalError, A]] with {
  def isZero(a: EvalResult[A]): Boolean = {
    a match {
      case Right(a) if summon[Numeric[A]].isZero(a) => true
      case _ => false
    }
  }

Finally we can implement the division operator for Numeric Either like this.

def div(a: EvalResult[A], b: EvalResult[A]): EvalResult[A] = {
  if isZero(b) then
    Left(EvalError.DivisionByZero)
  else 
    a.map2(b)(_ / _)
}

That's all for now, I hope you enjoyed this post and video. Please contact me using the methods above with any questions, suggestions or corrections!